Black holes and critical phenomena
A scalar field is a simple form of matter that feels two forces only, gravity produced by itself, and its own pressure. If you try to build a ball in which the field is initially weak, pressure wins and the ball expands away leaving nothing behind. If the field is initially strong gravity wins and the ball collapses to form a black hole.
There is a special critical initial strength such that the field cannot decide whether to evaporate away or collapse to form a black hole. Instead it oscillates increasingly rapidly, performing an infinite number of oscillations in a finite time. The two animations show first an evolution that doesn't form a black hole, and second an evolution which does. The initial strengths differ only by one in the fifteenth decimal place. Each frame shows the scalar field as a function of position. The gravitational field changes the frequency of the field and so the colour indicates what a distant observer would see.
• This evolution doesn't form a black hole.
• This collapse does form a black hole.
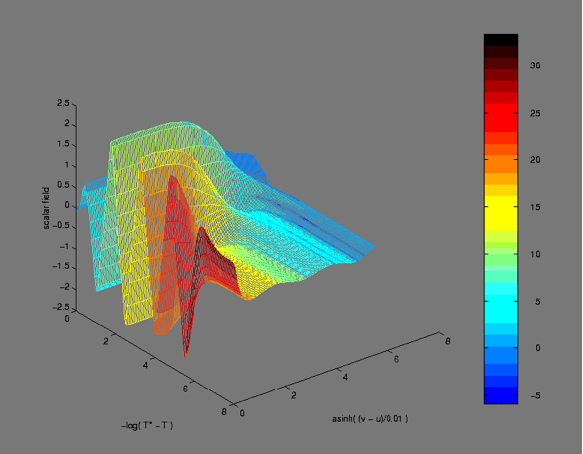
Because the animation moves so quickly it is hard to see what is happening. The picture on the right summarises the animations.
Time is increasing from left to right (downwards).
Radius is increasing from left to right (upwards).
The colour indicates the curvature of spacetime. Far away (back of picture) the spacetime is almost flat (blue) while on the axis the field is becoming stronger and stronger (red turning black). Although there are an infinite number of oscillations in a finite time, all bunched up on each other, we have stretched out the time coordinate to separate them.
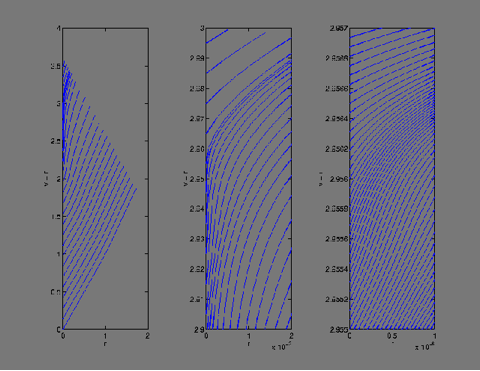
The next group of figures (below, left) show the paths of photons emitted from the axis. Each blue line in the left picture represents a photon path. Radius is plotted horizontally and time vertically. Thus photons emitted at late times have higher lines in the figure. In the first picture there is some fine detail near the axis. The second increases the scale by one thousand, and the third by a further one thousand. Here you can see that all the photons escape.
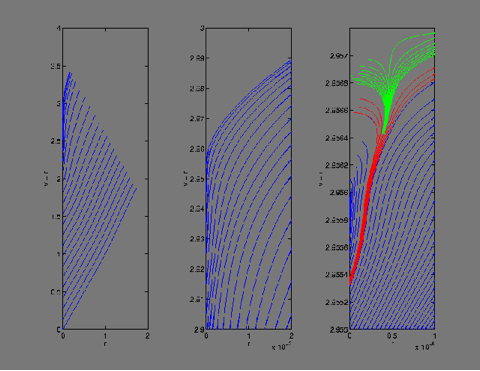
The other set (below, right) are the same photon paths but for the case where a black hole forms. At the finest resolution you can see that photons emitted at late times stop moving outwards and return back towards the axis. This is the moment at which the black hole forms.
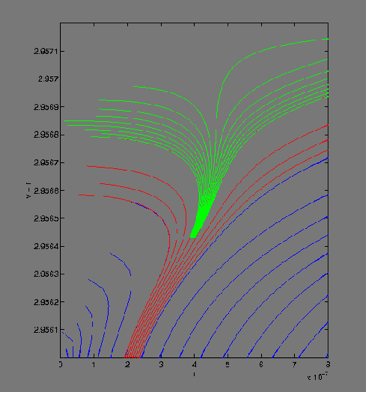
The figure on the left below is an enlargement of the area where a black hole forms. In the picture below on the right, we superpose the evolutions with (red) and without (green) black hole formation. At early times (bottom of the picture) the spacetimes differ only in the fifteenth decimal place. Once the spacetime decides what to do, the solutions then bifurcate.
We have seen here how a black hole forms, however, black holes will also eventually evaporate and disappear as well.