An introduction
Phase Transitions in the Early Universe
Towards the very early Universe...
As we move backwards in time towards the moment of creation, prior to one hundredth of a second, the Universe becomes hotter and denser until matter actually changes its phase, that is, it changes its form and properties. An everyday analogue familiar to all is simply water.
With increasing temperature we see a succession of phase transitions for water in which its properties change dramatically: the solid phase - ice - melts to the liquid phase - water - and then eventually boils to the gaseous phase - steam. You should notice that steam is 'more symmetric' than water, which is in turn more symmetric than ice (Can you see why? You can find an explanation below...). And so it is with matter in our Universe; it begins in a unified or 'symmetric' phase (as we will explain below) and then passes through a succession of phase transitions until, at lower temperatures, we finally obtain the matter particles with which physicists are familiar today: electrons, protons, neutrons, photons etc..
As we shall see in the next few pages, phase transitions may have had profound implications on the evolution of our Universe and its contents. Moreover, it is some direct 'remnants' of these transitions are still around today! The two key concepts of unification and phase transitions are vital to our present understanding of particle physics.
Unification
The basic premise of grand unification is that the known symmetries of the elementary particles resulted from a larger (and so far unknown) symmetry group G. Whenever a phase transition occurs, part of this symmetry is lost, so the symmetry group changes. This can be represented mathematically as
G -> H -> ... -> SU(3) x SU(2) x U(1) -> SU(3) x U(1).
Here, each arrow represents a symmetry breaking phase transition where matter changes form and the groups - G, H, SU(3), etc. - represent the different types of matter, specifically the symmetries that the matter exhibits and they are associated with the different fundamental forces of nature. These fundamental forces are the following:
- Electromagnetism: The group U(1) is associated with the electric and magnetic forces, that is, phenomena such as electricity and light. It was Maxwell's great achievement at the end of the nineteenth century to unify electric and magnetic effects into one single mathematical theory - electromagnetism.
- Weak nuclear force: This is the nuclear force associated with radioactivity in many unstable nuclei. In particular, it is associated with the decay of a neutron into a proton. The weak nuclear force was unified with electromagnetism by Weinberg and Salam in the late seventies, into what is known as electroweak theory and which is described by the group SU(2)xU(1). Predictions from this standard unified model were confirmed at the CERN particle accelerator in Geneva in the early 1980's.
- Strong nuclear force: The group SU(3) is associated with the strong nuclear force which binds together neutrons and protons inside nuclei. The mathematical theory describing the elementary particles in this theory – quarks (a group of six difference elementary particles, which combine to make protons and neutrons, amongst other things) and gluons - is known as quantum chromodynamics (QCD). The model is well understood in principle but, in practice, quantitative calculations prove to be very difficult. Models which unify the strong nuclear force with electroweak theory are known as grand unified theories or GUTs.
- Gravity: The weakest force of all - the gravitational force - is not included in the above scheme. The unification of the other fundamental forces with gravity is one of the great intellectual challenges facing theoretical physics. A number of possibilities exist, such as superstring theory, and they are known as TOEs, that is, theories of everything.
The analogue of water may again prove useful in understanding the concept of symmetry and symmetry breaking. The liquid phase of water is rotationally symmetric, that is, it looks the same around each point regardless of the direction in which we look. We could represent this large three-dimensional symmetry by the group G (actually SO(3)). The solid form of frozen water, however, is not uniform in all directions; the ice crystal has preferential lattice directions along which the water molecules align. The group describing these different discrete directions H, say, will be smaller than G. Through the process of freezing, therefore, the original symmetry G is broken down to H.
Phase transitions
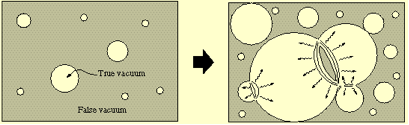
First order phase transitions proceed by bubble nucleation. A bubble of the new phase (the true vacuum) forms and then expands until the old phase (the false vacuum) disappears. A useful analogue is boiling water in which bubbles of steam form and expand as they rise to the surface
The cosmological significance of symmetry breaking is due to the fact that symmetries are restored at high temperature (just as it is for liquid water when ice melts). For extremely high temperatures in the early Universe, we will even achieve a grand unified state G. Viewed from the moment of creation forward, the Universe will pass through a succession of phase transitions at which the strong nuclear force will become differentiated and then the weak nuclear force and electromagnetism.
Phase transitions can have a wide variety of important implications including the formation of topological defects - cosmic strings, domain walls, monopoles and textures - that will be described in more detail in the following pages, or it may even trigger a period of exponential expansion (inflation). Our discussion of these effects will focus on the very early Universe, that is, in the earliest moments during the first one hundredth of a second after the Big Bang.
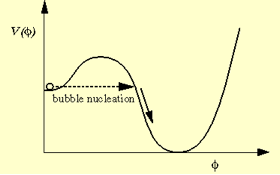
During a first-order phase transition, the matter fields get trapped in a 'false vacuum' state from which they can only escape by nucleating bubbles of the new phase, that is, the 'true vacuum' state
Phase transitions can be either dramatic - first order - or smooth - second order:
First-order phase transitions (illustrated above and to the left) occur through the formation of bubbles of the new phase in the middle of the old phase; these bubbles then expand and collide until the old phase disappears completely and the phase transition is complete.
Second-order phase transitions, on the other hand, proceed smoothly. The old phase transforms itself into the new phase in a continuous manner.
